Simples Rätsel, große Probleme: Nur die Hälfte kennt die Lösung

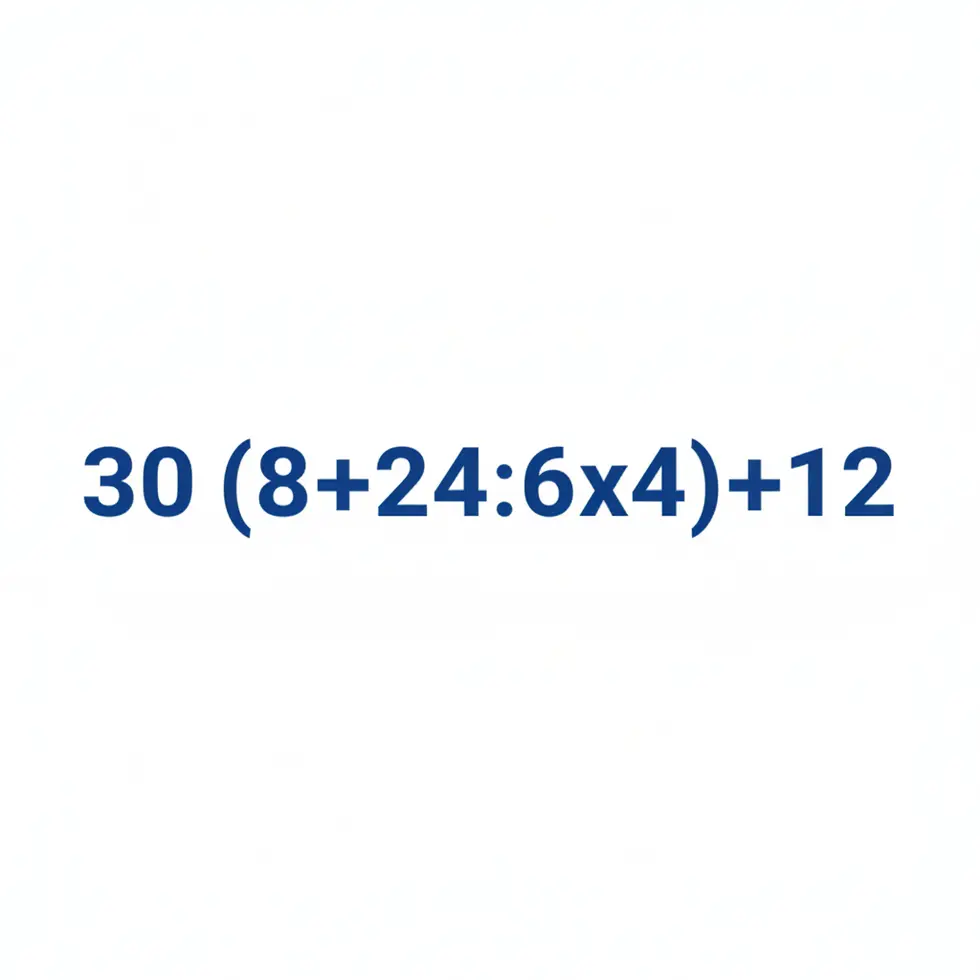
Es ist eine Szene, die sich täglich in den sozialen Medien abspielt: Ein Bild mit einer simplen mathematischen Gleichung taucht im Feed auf, versehen mit einer provokanten Frage wie „Nur Genies schaffen das!“ oder „90 % scheitern an dieser Aufgabe“. Die Kommentarspalten explodieren. Menschen streiten, werfen sich gegenseitig Unwissenheit vor und verteidigen vehement ihr Ergebnis. Das neueste Phänomen dieser Art ist eine auf den ersten Blick unscheinbare Aufgabe, die jedoch eine erstaunlich hohe Fehlerquote aufweist und eine tiefere Frage über unser verlerntes Wissen aufwirft.

Die Herausforderung lautet: 30 – (8 + 24 : 6 × 4) + 12. Eine simple Abfolge von Zahlen und Operatoren, wie man sie in der Mittelstufe lernt. Doch die Realität ist ernüchternd: Weniger als die Hälfte der Erwachsenen, die sich an der Lösung versuchen, kommen zum korrekten Ergebnis. Dieses Phänomen ist mehr als nur ein viraler Zeitvertreib; es ist ein faszinierender Einblick in die Psychologie des digitalen Zeitalters und ein Indikator dafür, wie grundlegende Fähigkeiten im Alltag verkümmern.

Warum wir an einfachen Regeln scheitern

Die Faszination solcher Rätsel liegt in ihrem trügerischen Charakter. Sie wirken einfach genug, um jeden zur Teilnahme zu verleiten, bergen aber eine versteckte Falle, die auf einem fundamentalen Prinzip der Mathematik beruht: der Operatorrangfolge. In Deutschland ist sie als „Klammer-Potenz-Punkt-vor-Strich-Rechnung“ bekannt, ein Mantra, das Lehrkräfte über Generationen hinweg vermittelt haben. Doch was im Klassenzimmer einst in Stein gemeißelt schien, verschwimmt im Erwachsenenalter oft zu einer vagen Erinnerung.

Die korrekte Vorgehensweise ist strikt hierarchisch. Zuerst werden die Operationen innerhalb der Klammer gelöst. Doch auch hier lauert die nächste Hürde. Innerhalb der Klammer `(8 + 24 : 6 × 4)` gilt die Regel „Punkt vor Strich“. Wir dürfen also nicht einfach von links nach rechts rechnen. Zuerst die Division: 24 : 6 = 4. Danach die Multiplikation: 4 × 4 = 16. Erst jetzt, nachdem alle Punktrechnungen erledigt sind, folgt die Strichrechnung in der Klammer: 8 + 16 = 24.

Mit diesem Zwischenergebnis wird die ursprüngliche Gleichung deutlich einfacher: `30 – 24 + 12`. An diesem Punkt machen viele den letzten Fehler. Sie sehen `24 + 12` und rechnen dies zuerst. Doch Addition und Subtraktion sind gleichrangig. In diesem Fall wird streng von links nach rechts gerechnet. Der korrekte nächste Schritt ist also: 30 – 24 = 6. Und schließlich: 6 + 12 = 18. Das richtige Ergebnis lautet 18.

Ein Spiegelbild unserer digitalen Abhängigkeit

Die hohe Fehlerquote ist weniger ein Zeichen mangelnder Intelligenz als vielmehr ein Symptom unserer Zeit. In einer Welt, in der jeder Taschenrechner, jedes Smartphone und jede Suchmaschine mathematische Probleme in Sekundenbruchteilen löst, haben wir das mentale Training verlernt. Dieses Phänomen wird in der Kognitionswissenschaft als „kognitives Offloading“ bezeichnet – die Auslagerung geistiger Anstrengungen an externe Werkzeuge. Das ist effizient, hat aber seinen Preis: Die neuronalen Pfade für grundlegende Fähigkeiten wie Kopfrechnen werden seltener genutzt und verkümmern langsam.

Diese Rätsel fungieren daher als eine Art informeller PISA-Test für Erwachsene. Sie decken schonungslos auf, wie weit sich viele von den Grundlagen entfernt haben, die das Fundament für komplexeres logisches Denken bilden. Die heftigen Debatten in den Kommentarspalten sind dabei besonders aufschlussreich. Sie zeigen nicht nur die Verunsicherung, sondern auch den Dunning-Kruger-Effekt in Aktion: Menschen mit geringerer Kompetenz neigen dazu, ihre Fähigkeiten zu überschätzen und halten ihr falsches Ergebnis hartnäckig für das einzig richtige. Sie argumentieren oft mit einer „Alltagslogik“, die in der präzisen Welt der Mathematik jedoch keine Geltung hat.

Aus einer deutschen und europäischen Perspektive ist dies besonders interessant. Das hiesige Bildungssystem legt traditionell großen Wert auf das Verständnis von Prinzipien und Strukturen, nicht nur auf das Auswendiglernen von Ergebnissen. Die Tatsache, dass selbst diese fundamentalen Regeln in Vergessenheit geraten, deutet auf eine Lücke zwischen schulischer Bildung und deren Anwendung im späteren Leben hin. Die Fähigkeit, eine solche Gleichung ohne Hilfsmittel zu lösen, ist kein reiner Selbstzweck. Sie ist ein Training für strukturiertes, regelbasiertes Denken – eine Kompetenz, die in der Programmierung, im Rechtswesen oder im Projektmanagement unerlässlich ist.

Letztlich ist dieses kleine mathematische Rätsel weit mehr als nur ein Spiel. Es ist eine harmlose, aber wirkungsvolle Erinnerung daran, dass Bequemlichkeit ihren Preis hat. Die virale Verbreitung und die kontroversen Diskussionen zeigen, dass tief in uns der Wunsch verankert ist, unsere geistigen Fähigkeiten zu testen und zu beweisen. Vielleicht ist der größte Wert dieser Online-Phänomene nicht die richtige Antwort selbst, sondern die landesweite Konversation über die Regeln, die unsere logische Welt zusammenhalten – und die Erkenntnis, dass es sich lohnt, diese von Zeit zu Zeit wieder aufzufrischen.